层状介质时间场模拟与报告

题目要求

已知一个简单的二维层状介质模型，模型横向长3500m，纵向深1000m。一水平界面的埋深为500m，界面上、下介质的速度分别是v1=2000m/s，v2=4000m/s。震源位于地表、距离左边界（400+你的学号后三位数X10）m处。 要求完成以下工作：

（1）设计一定的方法计算直达波、反射波、透射波、滑行波、折射波的时间场，按照0.05s间隔绘制时间场的等时线。

（2）根据各等时线到达地面各点的时间绘制直达波、反射波和折射波的时距曲线。
注意：距离比例尺为1:10000，即1cm代表100m；时间比例尺为1cm代表0.1s。

（3）编写《层状介质时间场模拟》研究报告，详细阐述所使用的方法原理、计算过程。要求至少阅读5篇相关的文献，并在研究报告中加以引用。

最终结果

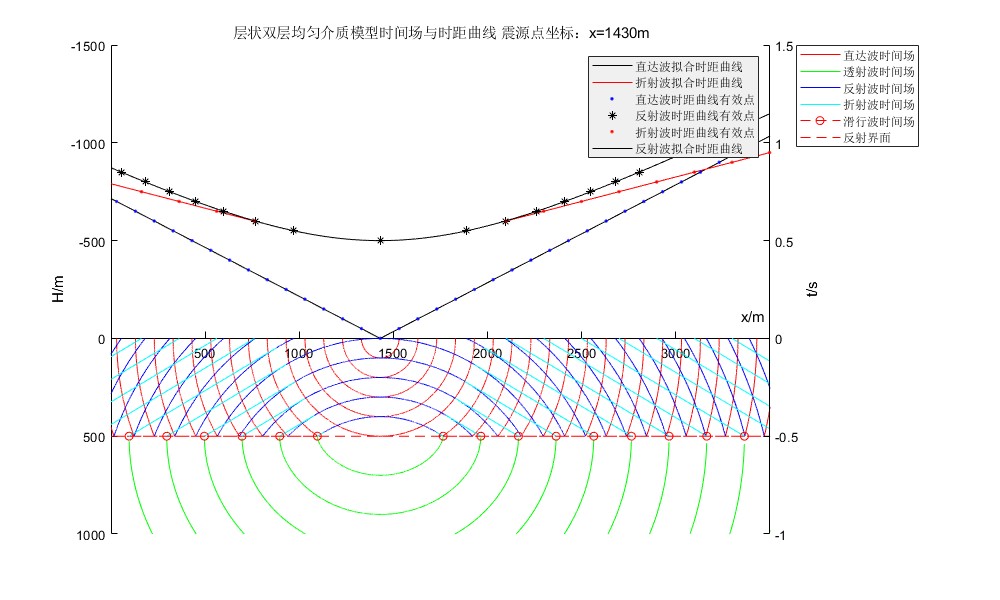
已知BUG

• 震源点坐标为100的整数倍时，会有左半部分直达波时距曲线缺失。
• 提高或降低时间场绘制精度时，出现绘制错误。

MATLAB代码

clc
clear

v1 = 2000;
v2 = 4000;
h1 = 500;  % 第一个界面深度
h2 = 1000;  % 最终深度
x1 = 2000;   % 震源点的横坐标
xmax = 3500; % 显示边界最大横坐标
xmin = 0;   % 显示边界最小横坐标
dangle = 0.01;
dt = 0.05;
sigma_C = asin(v1/v2);  % 存在透射波边界下的入射角


t_all = [ 0:dt:1.5];
N_t_all = length(t_all);
N = 180/dangle+1;
angle = zeros(1, N);
k = 0;
angle(1) = 0;
for i = 2:N  % 创建角度序列angle
    k = k + dangle;
    angle(i) = k;
end
angle = angle./180.*pi;

% 求取时间场有效点
[DW_x, DW_y, direct_time, k_dir]=direct_wave_count(angle, t_all, N_t_all, N, v1, h1, x1);%直达波
[tran_x,tran_y,one_tran_t] = transform_wave_count(angle, sigma_C, dt, N, v1,v2,h1,x1,xmax,xmin, direct_time, k_dir );%透射波
[reflect_x,reflect_y] = reflect_wave_count(angle, N, t_all, N_t_all, v1,h1,x1, direct_time, k_dir);%反射波
[refract_x_ri, refract_x_le,refract_y_ri, refract_y_le, refract_x, refract_y] = refract_wave_count(sigma_C, dt, t_all, N_t_all, v1,v2,h1,x1,xmax,xmin);%折射波
[slide_x, slide_y] = Slide__wave_count(t_all, N_t_all, v1, v2, h1, x1, sigma_C);

% 时间场绘图
h = figure(1);
h.Position = [0 0 1000 600];% 设置图片在显示器上的位置
hold on;
ax1 = gca;
set(ax1,'XColor','k','YColor','k');
INTERFACE = interface(xmax, xmin,h1);
DWH = image( DW_x, DW_y,'r-','直达波时间场');
TRH = image( tran_x, tran_y,'g-','透射波时间场');
REFLH = image( reflect_x, reflect_y,'b-','反射波时间场');   
REFRH = image( refract_x_ri, refract_y_ri,'c-', ' ');
REFRH = image( refract_x_le, refract_y_le,'c-','折射波时间场');
SLID=plot(slide_x, slide_y,'r--o','DisplayName','滑行波时间场');
set(gca, 'XAxisLocation', 'origin');
legend([DWH(1), TRH(1), REFLH(1), REFRH(1), SLID, INTERFACE],'Location','NorthEastOutside');
xlabel('x/m');
ylabel('H/m');

title(['层状双层均匀介质模型时间场与时距曲线 震源点坐标：x=',num2str(x1),'m']);

ax2 = axes('Position', get(ax1, 'Position'), 'YAxisLocation', 'right', 'Color', 'None', 'XColor', 'None', 'YColor', 'k');
set(ax2);
hold on

% 时距曲线绘图
DW_x_t = zeros(2,N_t_all);
tran_x_t = zeros(2,N_t_all);
reflect_x_t = zeros(2,N_t_all);
refract_x_t = zeros(2,N_t_all);
DW_x_t = t_x(DW_x, DW_y, DW_x_t, dangle);
reflect_x_t = t_x(reflect_x, reflect_y, reflect_x_t,dangle);
refract_x_t = t_x(refract_x, refract_y, refract_x_t,dangle);
axis([0,3500,-1.0,1.5]);

% 直达波拟合
[DW_T_FIT1, DW_T_FIT1_E]= polyfit(DW_x_t(1,:), t_all, 1);  % 2表示为x1右侧的曲线
DW_NEW_T = polyval(DW_T_FIT1, DW_x_t(1,:));
DW_T_FIT1=vpa(poly2sym(DW_T_FIT1));
plot(DW_x_t(1,:), DW_NEW_T, 'k-');

[DW_T_FIT2, DW_T_FIT2_E]= polyfit(DW_x_t(2,:), t_all, 1);
DW_NEW_T = polyval(DW_T_FIT2, DW_x_t(2,:));
DW_T_FIT2=vpa(poly2sym(DW_T_FIT2));
py1=plot(DW_x_t(2,:), DW_NEW_T, 'k-', 'DisplayName','直达波拟合时距曲线');


% 折射波拟合
x_effictive1 = [];
t_effictive1 = [];
x_effictive2 = [];
t_effictive2 = [];
[row, col]=size(refract_x_t);
for i=1:col
    if isnan(refract_x_t(1,i)) == 0
        x_effictive1 = [x_effictive1, refract_x_t(1,i)];
        t_effictive1 = [t_effictive1, t_all(i)];
    else
        continue
    end
end
for i=1:col
    if isnan(refract_x_t(2,i)) == 0
        x_effictive2 = [x_effictive2, refract_x_t(2,i)];
        t_effictive2 = [t_effictive2, t_all(i)];
    else
        continue
    end
end
[RER_T_FIT2, RER_T_FIT2_E]= polyfit(x_effictive1, t_effictive1, 1);
RER_NEW_T = polyval(RER_T_FIT2, x_effictive1);
RER_T_FIT2=vpa(poly2sym(RER_T_FIT2));
plot(x_effictive1, RER_NEW_T, 'r-');

[RER_T_FIT1, RER_T_FIT1_E]= polyfit(x_effictive2, t_effictive2, 1);
RER_NEW_T = polyval(RER_T_FIT1, x_effictive2);
RER_T_FIT1=vpa(poly2sym(RER_T_FIT1));
py2=plot(x_effictive2, RER_NEW_T, 'r-', 'DisplayName','折射波拟合时距曲线');
legend([py1, py2],'Location','NorthEast');

% 有效点绘制
plot([DW_x_t(2,:), DW_x_t(1,:)],[t_all, t_all], 'b.', 'DisplayName','直达波时距曲线有效点');
plot([reflect_x_t(1,:), reflect_x_t(2,:)],[t_all,t_all], 'k*','DisplayName','反射波时距曲线有效点');
plot([refract_x_t(1,:),refract_x_t(2,:)],[t_all, t_all], 'r.', 'DisplayName','折射波时距曲线有效点');

% 拟合反射波时距曲线为双曲线
[x_effictive, t_effictive, a, b]=reflect_wave_t_x([reflect_x_t(1,:), reflect_x_t(2,:)],[t_all,t_all], x1);
a=1/a;
b=1/b;
reflect_x_nihe = [xmin+1:1:xmax];
reflect_t_nihe = zeros(1,xmax);
for i= xmin+1:1:xmax
    reflect_t_nihe(i) = sqrt(a*(1+(reflect_x_nihe(i)-x1).^2/b));
end
plot(reflect_x_nihe, reflect_t_nihe, 'k-','DisplayName','反射波拟合时距曲线');
xlabel('x/m');
ylabel('t/s');
legend("show",'Location','NorthEast');

% 特殊点计算
fprintf("直达波拟合曲线方程：\n");
DW_T_FIT1
DW_T_FIT2
fprintf("直达波拟合曲线震源点右侧曲线残差范数：%f\n直达波拟合曲线震源点左侧曲线残差范数：%f\n", DW_T_FIT1_E.normr, DW_T_FIT2_E.normr);

fprintf("折射波拟合曲线方程：\n");
RER_T_FIT1
RER_T_FIT2
fprintf("折射波拟合曲线震源点右侧曲线残差范数：%f\n折射波拟合曲线震源点左侧曲线残差范数：%f\n", RER_T_FIT1_E.normr, RER_T_FIT2_E.normr);

fprintf("反射波拟合曲线方程：\n");
P=a;Q=b;R=x1;
REF_T_FIT=@(x)(P*(1+(x-R).^2/Q)).^(1/2);


% 直达波与折射波震源点右侧交点
DW_T_FIT1=matlabFunction(DW_T_FIT1);
RER_T_FIT1=matlabFunction(RER_T_FIT1);
DWRERZERO1=fsolve(@(x)(DW_T_FIT1(x)-RER_T_FIT1(x)), [x1, xmax]);
fprintf("直达波拟合时距曲线与折射波拟合时距曲线 震源点右侧交点x坐标值: %6.3f\n", DWRERZERO1(1));

% 直达波与折射波震源点左侧交点
DW_T_FIT2=matlabFunction(DW_T_FIT2);
RER_T_FIT2=matlabFunction(RER_T_FIT2);
DWRERZERO2=fsolve(@(x)(DW_T_FIT2(x)-RER_T_FIT2(x)), [xmin, x1]);

fprintf("直达波拟合时距曲线与折射波拟合时距曲线 震源点左侧交点x坐标值: %6.3f\n", DWRERZERO2(1));

% 折射波与震源点所在纵轴交点
fprintf("折射波拟合时距曲线与震源点所在纵轴交点t坐标值: %f、%f\n", RER_T_FIT1(x1),RER_T_FIT2(x1));
% 直达波与震源点所在纵轴交点
fprintf("直达波拟合时距曲线与震源点所在纵轴交点t坐标值: %f、%f\n", DW_T_FIT1(x1),DW_T_FIT2(x1));
% 反射波与震源点所在纵轴交点
fprintf("反射波拟合时距曲线与震源点所在纵轴交点t坐标值: %f\n", REF_T_FIT(x1));

% 折射波时距曲线与反射波时距曲线交点
REFRERZERO1=fsolve(@(x)(REF_T_FIT(x)-RER_T_FIT2(x)), [xmin, x1]);
REFERZERO2=fsolve(@(x)(REF_T_FIT(x)-RER_T_FIT1(x)), [x1, xmax]);
fprintf("折射波拟合左侧时距曲线与反射波时距曲线交点x坐标值: [%f \t%f]\n折射波拟合右侧时距曲线与反射波时距曲线交点x坐标值:[%f \t%f]\n", REFRERZERO1(:),REFERZERO2(:));


DW_T_THEO1=@(x)((x-x1)/v1); % 直达波时距曲线理论方程震源点右侧
DW_T_THEO2=@(x)(-(x-x1)/v1); % 直达波时距曲线理论方程震源点左侧

RER_T_THEO1=@(x)((x-x1)/v2+2*h1*cos(sigma_C)/v1); % 折射波时距曲线理论方程震源点右侧
RER_T_THEO2=@(x)(-(x-x1)/v2+2*h1*cos(sigma_C)/v1); % 折射波时距曲线理论方程震源点左侧


REF_T_THEO=@(x)(((2*h1/v1).^2*(1+(x-x1).^2/((2*h1).^2))).^(1/2)); % 反射波时距曲线理论方程

% 折射波理论时距曲线与直达波理论时距曲线交点
DWRER_THEO_ZERO1=fsolve(@(x)(DW_T_THEO1(x)-RER_T_THEO1(x)), [x1, xmax]);
fprintf("折射波理论时距曲线与直达波理论时距曲线震源点右侧交点x坐标值: %f\n", DWRER_THEO_ZERO1(1));

DWRER_THEO_ZERO2=fsolve(@(x)(DW_T_THEO2(x)-RER_T_THEO2(x)), [xmin, x1]);
fprintf("折射波理论时距曲线与直达波理论时距曲线震源点左侧交点x坐标值: %f\n", DWRER_THEO_ZERO2(1));

% 折射波理论时距曲线与反射波理论时距曲线交点
REF_THEO_ZERO1=fsolve(@(x)(REF_T_THEO(x)-RER_T_THEO1(x)), [x1, xmax]);
fprintf("折射波理论时距曲线与直达波理论时距曲线震源点右侧交点x坐标值: %f %f\n", REF_THEO_ZERO1);
REF_THEO_ZERO2=fsolve(@(x)(REF_T_THEO(x)-RER_T_THEO2(x)), [xmin, x1]);
fprintf("折射波理论时距曲线与直达波理论时距曲线震源点左侧交点x坐标值: %f %f\n", REF_THEO_ZERO2);

fprintf("直达波理论时距曲线与震源点所在纵轴交点t坐标值: %f、%f\n", DW_T_THEO1(x1),DW_T_THEO2(x1));
fprintf("折射波理论时距曲线与震源点所在纵轴交点t坐标值: %f、%f\n", RER_T_THEO1(x1),RER_T_THEO2(x1));
fprintf("反射波理论时距曲线与震源点所在纵轴交点t坐标值: %f\n", REF_T_THEO(x1));

%% 直达波时间场计算
function [DW_x, DW_y, direct_time,k_dir] = direct_wave_count(angle, t_all, N_t_all, N, v1,h1,x1)

    k_dir = tan(angle);   % 斜率计算
    DW_x = zeros(N, N_t_all);  % 存储所有射线和时间的x值 纵坐标为angle，横坐标为time
    DW_y = zeros(N, N_t_all);
    for i = 1 : N  % angle循环
        for j = 1 : N_t_all  % time循环
            if angle(i) < pi/2
                x = x1 + ( (v1*t_all(j))^2/(1 + k_dir(i)^2))^0.5;
                if k_dir(i)*(x - x1) < h1 
                    DW_x(i, j) = x;
                    DW_y(i, j) = k_dir(i)*(x - x1);
                else
                    DW_x(i, j) = NaN;  % 将不需要的x值删去
                    DW_y(i, j) = NaN;
                end
            elseif angle(i) > pi/2
                x = x1 - ((v1*t_all(j))^2/(1 + k_dir(i)^2))^0.5;
                if k_dir(i)*(x - x1) < h1
                    DW_x(i, j) = x;
                    DW_y(i, j) = k_dir(i)*(x - x1);
                else
                    DW_x(i, j) = NaN;
                    DW_y(i,j) = NaN;
                end
            elseif angle(i) == pi/2
                DW_x(i, j) = x1;
                DW_y(i,j) = t_all(j)*v1;
            end
    
        end
    end
    
    direct_time = zeros(1, N);  % 计算各个角度波抵达h1边界的时间
    for i = 1 : N
        if angle(i) >= 0 && angle(i) <= pi
            direct_time(i) = h1 / v1 / abs(sin(angle(i)));
        else
            direct_time(i) = NaN;
        end
    end
end

%% 透射波时间场计算
function [tran_x,tran_y,one_tran_t] = transform_wave_count(angle, sigma_C, dt, N, v1,v2,h1,x1,xmax,xmin, direct_time, k_dir )
    anglep = angle;
    for i = 1 :N
        if angle(i)<= pi/2+sigma_C && angle(i) >= pi/2-sigma_C
            anglep(i) = angle(i);
        else
            anglep(i) = NaN;
        end
    end
    
    sigma = anglep - pi/2;   % sigma是边界之内的入射角
    beta = asin(v2/v1.*sin(sigma)); % beta是入射角对应的透射角
    
    k_tran = zeros(1,N);  % 透射波射线斜率
    for i = 1 :N
        if beta(i) <= pi/2
            k_tran(i) = tan(pi/2-beta(i));
        else
            k_tran(i) = -tan(pi/2-beta(i));
        end
    end
    
    t_min = h1/v1;      % 透射波出现时的最早时间
    
    N_tran = 10;
    one_tran_t = zeros(1, N_tran);   % 透射波可以只画出几条曲线即可
    for i=1:N_tran
        one_tran_t(i) = floor(t_min/dt)*dt + dt * i;
    end
    
    tran_x = zeros(N, N_tran);
    tran_y = zeros(N, N_tran);
    for i=1 : N   % angle循环
        if anglep(i)<= pi/2+sigma_C && anglep(i) >= pi/2-sigma_C
            for  j = 1 : N_tran  % 时间循环
                if (one_tran_t(j) - direct_time(i)) >= 0  
                    if angle(i) ~= pi/2
                        tran_x(i,j) = x1+h1/k_dir(i)-v2*sin(beta(i))*(one_tran_t(j)-direct_time(i));
                        tran_y(i,j) = h1+v2*cos(beta(i))*(one_tran_t(j)-direct_time(i));
                    else
                        tran_x(i,j) = x1;
                        tran_y(i,j) = h1+v2*(one_tran_t(j) - direct_time(i));
                        continue
                    end
                else
                    tran_x(i,j) = NaN;  % 当该点不符合要求时为NaN，绘图时不予考虑
                    tran_y(i,j) = NaN;
                end
            end
        else
            tran_x(i,:) = NaN;
            tran_y(i,:) = NaN;
        end
    end
end
%% 反射波时间场计算
function [reflect_x,reflect_y] = reflect_wave_count(angle, N, t_all, N_t_all, v1, h1, x1, direct_time, k_dir )
    rx = h1./k_dir+x1;
    sigma = angle - pi/2;%重新设置sigma角度
    alpha = -sigma; % 反射角
    reflect_x = zeros(N, N_t_all);
    reflect_y = zeros(N, N_t_all);
    reflect_t = zeros(N, N_t_all);
    for i = 1:N
        for j = 1:N_t_all
            reflect_t(i,j) = t_all(j);
        end
    end
    for i = 1:N
        for j = 1 :N_t_all
            if (t_all(j)-direct_time(i))>=0
                reflect_x(i,j) = rx(i)+v1*sin(alpha(i))*(t_all(j)-direct_time(i));
                reflect_y(i,j) = h1-v1*cos(alpha(i))*(t_all(j)-direct_time(i));
                if reflect_y(i,j) < 0  % 超过地表的反射波设置为NaN
                    reflect_x(i,j)=NaN;
                    reflect_y(i,j)=NaN;
                else
                    continue
                end
            else
                reflect_x(i,j) = NaN;
                reflect_y(i,j) = NaN;
            end
        end
    end
end
%% 折射波时间场计算
function  [refract_x_ri, refract_x_le,refract_y_ri, refract_y_le, refract_x, refract_y]= refract_wave_count(sigma_C, dt, t_all, N_t_all, v1,v2,h1,x1,xmax,xmin)
    xr_min_ri = x1+h1*tan(sigma_C);  % 出现折射波的x1点右侧最小x值
    xr_max_le = x1-h1*tan(sigma_C); %出现折射波的x1点左侧最大x值
    t_rmin = h1/v1/cos(sigma_C);
    dx=1; % 所取射线的间隔   
    % 重新构造每一条折射波射线所过的点 
    N_refract_ri = ceil((xmax-x1-h1*tan(sigma_C))/dx)*10;
    N_refract_le = ceil((x1-h1*tan(sigma_C)-xmin)/dx)*100;
    xr_ri = zeros(1,N_refract_ri);
    xr_le = zeros(1,N_refract_le);
    for i=1:N_refract_ri
        xr_ri(i) = xr_min_ri + dx*(i-1);
    end
    for i=1:N_refract_ri
        xr_le(i) = xr_max_le - dx*(i-1);
    end
    % 求取每一条射线在一定时间时到达的点
    refract_x_ri = zeros(N_refract_ri,N_t_all);
    refract_x_le = zeros(N_refract_le,N_t_all);
    refract_y_ri = zeros(N_refract_ri,N_t_all);
    refract_y_le = zeros(N_refract_le,N_t_all);
    for i = 1:N_refract_ri
        for j = 1:N_t_all
            if (t_all(j)-t_rmin-(xr_ri(i)-xr_min_ri)/v2)>=0
                refract_x_ri(i,j) = xr_ri(i)+v1*sin(sigma_C)*(t_all(j)-t_rmin-(xr_ri(i)-xr_min_ri)/v2);
                refract_y_ri(i,j) = h1-v1*cos(sigma_C)*(t_all(j)-t_rmin-(xr_ri(i)-xr_min_ri)/v2);
                 if refract_y_ri(i,j) <0 || refract_y_ri(i,j)>h1
                    refract_x_ri(i,j) = NaN;
                    refract_y_ri(i,j) = NaN;
                else
                    continue
                end
            else
                refract_x_ri(i,j) = NaN;
                refract_y_ri(i,j) = NaN;
            end
        end
    end
    
    for i = 1:N_refract_le
        for j = 1:N_t_all
            if t_all(j)-t_rmin+(xr_le(i)-xr_max_le)/v2>=0
                refract_x_le(i,j) = xr_le(i)-v1*sin(sigma_C)*(t_all(j)-t_rmin+(xr_le(i)-xr_max_le)/v2);
                refract_y_le(i,j) = h1-v1*cos(sigma_C)*(t_all(j)-t_rmin+(xr_le(i)-xr_max_le)/v2);
                if refract_y_le(i,j) <0 || refract_y_le(i,j)>h1
                    refract_x_le(i,j) = NaN;
                    refract_y_le(i,j) = NaN;
                else
                    continue
                end
            else
                refract_x_le(i,j) = NaN;
                refract_y_le(i,j) = NaN;
            end
        end
    end
    
    refract_x = [refract_x_le; refract_x_ri];  % 合并以方便绘图
    refract_y = [refract_y_le; refract_y_ri];
end

%% 滑行波时间场计算
function [slide_x, slide_y] = Slide__wave_count(t_all, N_t_all, v1, v2, h1, x1, sigma_C)
    slide_x_ri=zeros(1,N_t_all);
    slide_x_le=zeros(1,N_t_all);
    slide_y_ri=h1*ones(1,N_t_all);
    slide_y_le=h1*ones(1,N_t_all);
    for i = 1:N_t_all
        if (t_all(i)-h1/(v1*cos(sigma_C)))>=0
            slide_x_ri(i)=x1+h1*tan(sigma_C)+v2*(t_all(i)-h1/(v1*cos(sigma_C)));
            slide_x_le(i)=x1-h1*tan(sigma_C)-v2*(t_all(i)-h1/(v1*cos(sigma_C)));
        else
            slide_x_ri(i)=NaN;
            slide_x_le(i)=NaN;
        end
    end
    slide_x = [slide_x_le, slide_x_ri];
    slide_y = [slide_y_le, slide_y_ri];
end

%% 时间场绘图函数
function H = image( x, y, color, Name)   
    [~, N_all] = size(x);
    H=zeros(1, N_all);
    for i = 1 : N_all
        x_dir = x(:,i).';
        y_dir = y(:,i).';
        H(i)=plot(x_dir, y_dir, color, 'DisplayName', Name);
    end
    
end

%% 时距曲线点计算
function x_t = t_x(x,y,x_t,dangle)   % 计算时距曲线的相关点
    [N,N_t_all]=size(x); 
    x_t(1,1)=x(1);
    y_test=100*ones(2,N_t_all);  %设置一个测试值
    for j=1:N_t_all
        for i=1:floor(N/2)
            if y(i,j)<=18*dangle  % 由于精度问题，当y<一定值的时候可以认为它出射地表
                if abs(y(i,j))<=abs(y_test(1,j)) % 如果有比它更优的点，择取最优值
                    x_t(1,j)=x(i,j);  
                    y_test(1,j) = y(i,j);
                else
                    continue
                end
            else
                continue
            end
        end
        for i=floor(N/2)-1:N
            if y(i,j)<=20*dangle
                if abs(y(i,j))<=abs(y_test(2, j))
                    x_t(2,j)=x(i,j);
                    y_test(2, j) = y(i,j);
                else
                    continue
                end
            else
               continue
            end
        end
    end
    for j=1:N_t_all
        for i=1:2
            if x_t(i,j) == 0
                x_t(i,j) = NaN;
            else
                continue
            end
        end
    end
end

%% 反射波拟合函数，对反射波进行双曲线拟合，得到一条光滑曲线
function [x_effictive,t_effictive, a, b]=reflect_wave_t_x(x,t, x1)  
    x_effictive = [];
    t_effictive = [];
    for i=1:length(x)
        if isnan(x(i)) == 0
            x_effictive = [x_effictive, x(i)];
            t_effictive = [t_effictive, t(i)];
        else
            continue
        end
    end
    K = floor(length(x_effictive)/2);
    A=zeros(1,K);
    B=zeros(1,K);
    for i=1:K
        A(i)=(-(x_effictive(i+K)-x1).^2+(x_effictive(i)-x1).^2)/(-(x_effictive(i+K)-x1).^2*t_effictive(i).^2+(x_effictive(i)-x1).^2*t_effictive(i+K).^2);
        B(i)=(-t_effictive(i+K).^2+t_effictive(i).^2)/(-(x_effictive(i+K)-x1).^2*t_effictive(i).^2+(x_effictive(i)-x1).^2*t_effictive(i+K).^2);
    end
   a=mean(A);
   b=mean(B);
end

%% 反射界面绘制函数
function INTER = interface(xmax, xmin,h1)
    xx = zeros(1,(xmax-xmin)/0.01);
    for i = 1:(xmax-xmin)/0.01
        xx(i) = i*0.01;
    end
    INTER = plot(xx, h1*ones(1,(xmax-xmin)/0.01), 'r--','DisplayName','反射界面');
    set(gca,'YDir','reverse', 'XAxisLocation', 'top');
    axis([xmin,xmax,-1500,1000]);
end

报告

下载链接